|

|
Christian Johann Doppler, 1803–53
Austrian physicist. He was born in Salzburg as the son of a stone-mason. Finished Vienna Polytechnic University and remain work there on reader position till 1835 yr, when got offer to head of chair of Math in Prague University . That event forced him to change his decision to emigrate to America , which he adopted because he lost all hopes to draw a confession in scientific community of motherland. He finished his career as professor of Royal imperial University of Vienna .
|
Shortly the idea of Doppler's effect is :
• if you move in direction to the source of emanation, the frequency of emanation for you increases.
• if you move in direction from the source of emanation, the frequency of emanation for you decreases.
For our case :
• The satellite rises, approaching to antenna, so frequency of satellite's transmitter increases for us till upper point (zenith).
• The satellite passes upper point (zenith) and begin to set, thereby goes out from antenna, frequency of satellite's transmitter decreases for us.
Well, if you don't understand – there is the example from the life :
Do you ever stay at the wayside in moment when there goes the car with buzzer turning on ? I think – yes. So recall the sound of buzzer : when car draw closer to you the sound sounds higher, and , after car overtake you and go out from you, the sound sounds lower and you hear familiar : ‘yyyyeeeeeEAAAAAOoooouuuummmmm'. That time, may be not realize it completely, you observed that waves's property.
Well, if you don't understand it again, and you are math, there is one more method of explanation of Doppler's effect :
Let see the simple case, when speed of the source ? È and speed of observer ? Í relative of the environment, directs along the straight which unite them. Let take the direction from observer to source as positive for ? È è ? Í . The speed of sound always is positive.
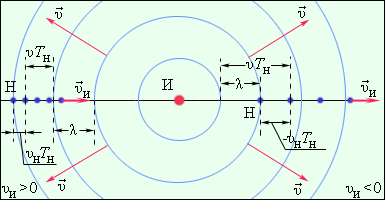
Fig 2.8.1
Doppler's effect. The case of the moving observer.
Sequential positions of observer shows via period T of sound, received by observer.
Fig 2.8.1 illustrated the Doppler effect in case of moving observer and motionless source. The period of sound waves, receiving by observer signed as T Í . From Fig 2.8.1 follows :
? Í T Í + ?T Í = ?.
Taking in attention  and and  we got : we got :

If observer moves to the source ( ? Í > 0), then f Í > f È , if observer moves from source ( ? Í < 0), then f Í < f È .
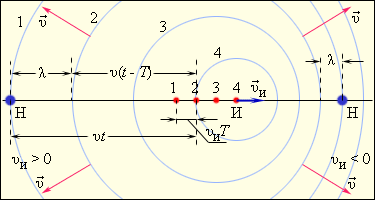
Fig 2.8.2
Doppler's effect. The case of the moving source
Sequential positions of source shows via period T of sound, emitted by source.
On the Fig 2.8.2 observer is motionless, but source move with some speed ? È . In this case, according Fig 2.8.2, the relation
? t + ? È T = ? (t – T) + ? èëè ( ? È + ? )T = ? , |
where  è è  is true. is true.
This implies :
If source move out from observer, ? È > 0 and, in that way, f Í < f È . If source approaches to observer then ? È < 0 è f Í > f È .
In common case, when source and observer both moved with speed ? È è ? Í , the formula for Doppler effect looks like :

This formula express relation between f Í è f È . Speeds ? È è ? Í has always measured relative air or another environment, where sound waves can propagate. This is so-called non-relativistic Doppler-effect.
In case of electromagnetic waves in vacuum (light, radio-waves) the Doppler-effect observed also. As for propagate of electromagnetic waves the material environment is not necessary, we can analyze the relative speed of source and observer only.
The formula for relativistic Doppler-effect looks like :

where c – velocity of light. When ? > 0, the source moves out of observer and f Í < f È , in case u<0 source moves to observer and f Í > f È .
Doppler-effect widely used in tech for measure the speed of running objects (“Doppler location” in acoustics, optics and radio)
If you don't understand it again, just gob on it, that Doppler's effect. It is not necessary to you.
|